【問題の例】
Aさんは午前10時に家を出て、1200mはなれた駅に向かいました。
そして途中にある郵便局の前で右に曲がり、そこから100mはなれたところのおじいさんの家へ預かり物をとりに行ったあと、また郵便局の前まで戻って、駅へと向かいました。
電車の時間が気になったので、郵便局の前からは、もとの速さの1.5倍にあたる分速90mで早歩きしたところ、家を出てから20分で駅に着きました。
Aさんの家から郵便局までの道のりを求めなさい。
ただし、おじいさんの家で預り物を受け取った時の時間は、計算に含めません。
家から郵便局までの道のりをXmとする。
すると、郵便局から駅までは、(1200-X)mとなる。
また、郵便局の前からおじいさんの家までは片道100メートルの往復なので、もとの速さで歩いた道のりは、(X+100×2)となる。
もとの速さは、90÷1.5=60、分速60mである。これだけの条件を整理して、式を立てると
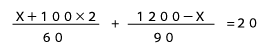
【解答】
これを、両辺に180をかけて解くと
3X+600+2400-2X=3600
3X-2X=3600-600-2400
X=600 A.600m となる。
式さえ立ててしまえば、少しも難しくない一次方程式です。
が、問題文がやや長いので、赤字のひとつ目、郵便局からおじいさんの家まで行き、まっすぐ往復して、またもとの(家からの)道のつづきを駅まで歩いて行くだけだ、というAさんの行動がよく理解できず、混乱してしまう子が多くいます。
こうした問題文で大きく戸惑うか、すぐに理解できるか、ということに「国語力」が大きく影響していることは、よくおわかりいただけると思います(青字部分は、数学の鉄則です)。
※もちろん数学の授業では、以下のように図示して解説します。
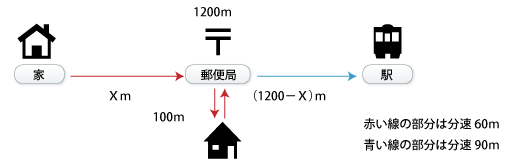
こうして図式化することができる前提に、文章からAさんの行動をイメージする「国語力」があるのです。
この「読みとる力」がしっかりしていると、図式のパターンが変わっても、自分で「図式化」することができます。
今の時代はあまりにも、いろいろなものが図式化、視覚化されすぎているため、「文章」から「正確なイメージ」を組み立てることが難しくなっているのかも知れません。
ちなみに上の例題を作問して今在籍している中学生たちに解かせてみたところ、その子たちの中で題意をすんなりと読みとることができたのは(郵便局の前からおじいさんの家まで往復するところと、赤字部分の分速60mについて)、小学校時代から在籍していて国語の「音読」の授業を長く受けた経験のある生徒でした。